SkipList总结

skiplist简介

skip List是一种随机化的数据结构，基于并联的链表，实现简单，插入、删除、查找的复杂度均为O(logN)（大多数情况下），因为其性能匹敌红黑树且实现较为简单，因此在很多著名项目都用跳表来代替红黑树，例如LevelDB、Redis的底层存储结构就是用的SkipList。
目前常用的key-value数据结构有三种：Hash表、红黑树、SkipList，它们各自有着不同的优缺点：
Hash表：插入、查找最快，为O(1)；如使用链表实现则可实现无锁；数据有序化需要显式的排序操作。
红黑树：插入、查找为O(logn)，但常数项较小；无锁实现的复杂性很高，一般需要加锁；数据天然有序。
SkipList：插入、查找为O(logn)，但常数项比红黑树要大；底层结构为链表，可无锁实现；数据天然有序。

SkipList基本数据结构及其实现

一个跳表，应该具有以下特征：

1、一个跳表应该有几个层（level）组成；
通常是10-20层，leveldb中默认为12层。

2、跳表的第0层包含所有的元素；
且节点值是有序的。

3、每一层都是一个有序的链表；
层数越高应越稀疏，这样在高层次中能’跳过’许多的不符合条件的数据。

4、如果元素x出现在第i层，则所有比i小的层都包含x；

5、每个节点包含key及其对应的value和一个指向该节点第n层的下个节点的指针数组
x->next[level]表示第level层的x的下一个节点

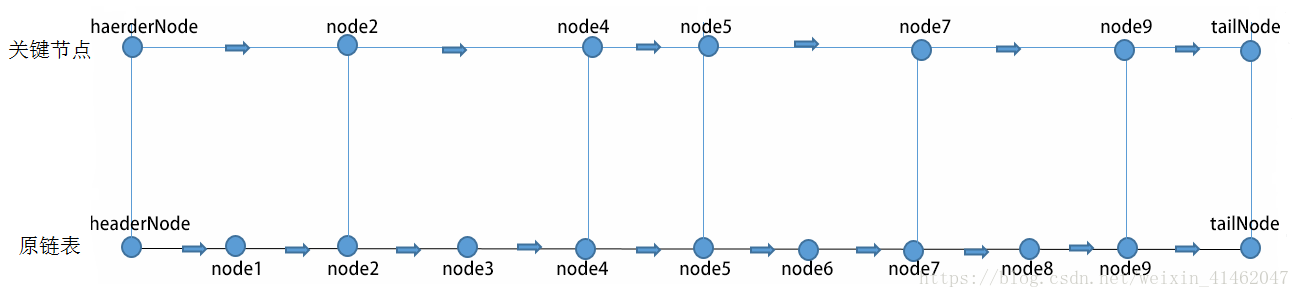
一个有序的链表，我们选取它的一半的节点用来建索引，这样如果插入一个节点，我们比较的次数就减少了一半。这种做法，虽然增加了50%的空间，但是性能提高了一倍。如上图。既然，我们已经提取了一层节点索引，那么，可以在第一层索引上再提取索引。如下图。

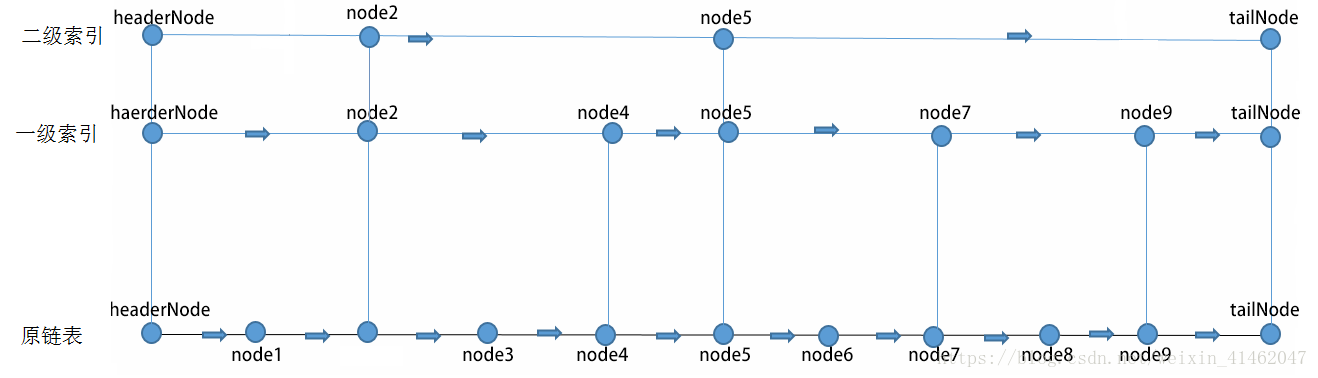
对于node5来说，它的next：

node5->next[2] = tailNode;
node5->next[1] = node7;
node5->next[0] = node6;

对于node7来说，它的next：

node7->next[1] = node9;
node7->next[0] = node8;

对于node3来说，它的next：

node3->next[0] = node4;

skiplist查找

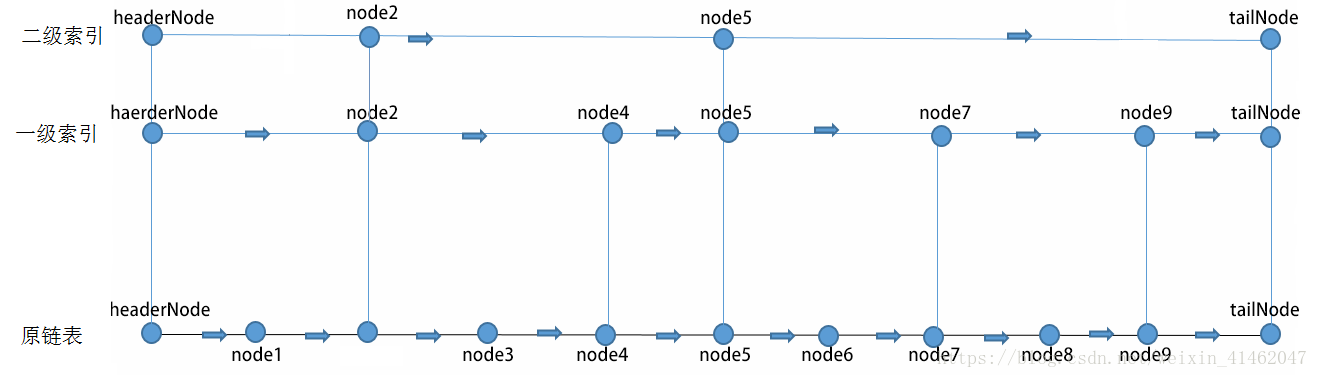
综上：
当targetNode->next[i]的值 < 待查找的值时，令targetNode = targetNode->next[i]，targetNode移到第i级的下一个结点；
当targetNode->next[i]的值 > 待查找的值时，向下降级，i- - ，不改变targetNode；
当targetNode->next[i]的值 = 待查找的值时，向下降级，i- - ，不改变targetNode。
最后，再次比较targetNode->next[0]和theElement，判断是否找到。
所以整个运算下来，targetNode是要查找的节点前面那个节点。

/* 如果存在 x, 返回 x 所在的节点， 
 * 否则返回 x 的后继节点 */  
find(x)   
{  
    p = top;  
    while (1) {  
        while (p->next->key < x)  
            p = p->next;  
        if (p->down == NULL)   
            return p->next;  
        p = p->down;  
 }

skiplist插入

插入的步骤：
新节点和各层索引节点逐一比较，确定原链表的插入位置。O（logN）
把索引插入到原链表。O（1）
利用抛硬币的随机方式，决定新节点是否提升为上一级索引。结果为“正”则提升并继续抛硬币，结果为“负”则停止。O（logN）
总体上，跳表插入操作的时间复杂度是O（logN），而这种数据结构所占空间是2N，既空间复杂度是 O（N）。

skiplist删除

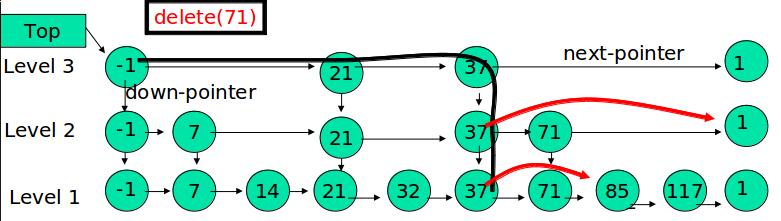
自上而下，查找第一次出现节点的索引，并逐层找到每一层对应的节点。O（logN）
删除每一层查找到的节点，如果该层只剩下1个节点，删除整个一层（原链表除外）。O（logN）
总体上，跳表删除操作的时间复杂度是O（N）

skiplist实现

package com.hqq.list;

import java.net.CacheRequest;

/**
 * SkipListNode
 * 跳跃表的节点,包括key-value和上下左右4个指针
 * Created by heqianqian on 2017/6/1.
 */
public class SkipListNode<T> {
    private int key;
    private T value;
    public SkipListNode<T> up, down, left, right;

    public static final int HEAD_KEY = Integer.MIN_VALUE;//负无穷
    public static final int TAIL_KEY = Integer.MAX_VALUE;//正无穷

    public SkipListNode(int k, T v) {
        this.key = k;
        this.value = v;
    }

    public int getKey() {
        return key;
    }

    public void setKey(int key) {
        this.key = key;
    }

    public T getValue() {
        return value;
    }

    public void setValue(T value) {
        this.value = value;
    }

    @SuppressWarnings("unchecked")
    public boolean equals(Object o) {
        if (this == o) {
            return true;
        }
        if (o == null) {
            return false;
        }
        if (!(o instanceof SkipListNode<?>)) {
            return false;
        }

        SkipListNode<T> ent;
        try {
            ent = (SkipListNode<T>) o;
        } catch (Exception e) {
            return false;
        }
        return (ent.getKey() == key) && (ent.getValue() == value);
    }

    @Override
    public String toString() {
        return "key-value:"+key+"-"+value;
    }
}

package com.hqq.list;

import java.util.Comparator;
import java.util.Random;

/**
 * SkipList
 * 不固定层级的跳跃表
 * Created by heqianqian on 2017/6/1.
 */
public class SkipList<T extends Comparable<? super T>> {

    private SkipListNode<T> head, tail;
    private int nodes;//节点总数
    private int listLevel;//层数
    private Random random;//用于产生随机数
    private static final double PROBABILITY = 0.5;//向上提升一个的概率

    public SkipList() {
        random = new Random();
        clear();
    }

    /**
     * 清空跳跃表
     */
    public void clear() {
        head = new SkipListNode<T>(SkipListNode.HEAD_KEY, null);
        tail = new SkipListNode<T>(SkipListNode.TAIL_KEY, null);
        horizontalLink(head, tail);
        listLevel = 0;
        nodes = 0;
    }

    /**
     * 水平双向连接
     */
    private void horizontalLink(SkipListNode<T> node1, SkipListNode<T> node2) {
        node1.right = node2;
        node2.left = node1;
    }

    /**
     * 垂直双向连接
     */
    private void vertiacallLink(SkipListNode<T> node1, SkipListNode<T> node2) {
        node1.down = node2;
        node2.up = node1;
    }

    /**
     * 在最下面一层，找到要插入的位置前面的那个key
     */
    private SkipListNode<T> findNode(int key) {
        SkipListNode<T> p = head;
        while (true) {
            while (p.right.getKey() != SkipListNode.TAIL_KEY && p.right.getKey() <= key) {
                p = p.right;
            }
            if (p.down != null) {
                p = p.down;
            } else {
                break;
            }
        }
        return p;
    }

    /**
     * 查找是否存储key，存在则返回该节点，否则返回null
     */
    public SkipListNode<T> search(int key) {
        SkipListNode<T> p = findNode(key);
        return (key == p.getKey()) ? p : null;
    }

    /**
     * 向跳跃表中添加key-value
     */
    public void put(int k, T v) {
        SkipListNode<T> p = findNode(k);
        //如果key值相同，替换原来的vaule即可结束
        if (k == p.getKey()) {
            p.setValue(v);
            return;
        }
        SkipListNode<T> q = new SkipListNode<T>(k, v);
        backLink(p, q);
        int currentLevel = 0;//当前所层次是0
        //产生随机数
        while (random.nextDouble() < PROBABILITY) {
            //新建一个层
            if (currentLevel >= listLevel) {
                listLevel++;
                SkipListNode<T> p1 = new SkipListNode<T>(SkipListNode.HEAD_KEY, null);
                SkipListNode<T> p2 = new SkipListNode<T>(SkipListNode.TAIL_KEY, null);
                horizontalLink(p1, p2);
                vertiacallLink(p1, head);
                vertiacallLink(p2, tail);
                head = p1;
                tail = p2;
            }
            //把p移动到上一层
            while (p.up == null) {
                p = p.left;
            }
            p = p.up;

            SkipListNode<T> e = new SkipListNode<T>(k, null);
            backLink(p, e);
            vertiacallLink(e, q);
            q = e;
            currentLevel++;
        }
        nodes++;
    }

    /**
     * 在node1后插入node2
     */
    private void backLink(SkipListNode<T> node1, SkipListNode<T> node2) {
        node2.left = node1;
        node2.right = node1.right;
        node1.right.left = node2;
        node1.right = node2;
    }

    public boolean isEmpty() {
        return nodes == 0;
    }

    public int size() {
        return nodes;
    }

    @Override
    public String toString() {
        if (isEmpty()) {
            return "跳跃表为空";
        }
        StringBuilder builder = new StringBuilder();
        SkipListNode<T> p = head;
        while (p.down != null) {
            p = p.down;
        }
        while (p.left != null) {
            p = p.left;
        }
        if (p.right != null) {
            p = p.right;
        }
        while (p.right != null) {
            builder.append(p);
            builder.append("\n");
            p = p.right;
        }
        return builder.toString();
    }
}

参考文章

• https://blog.csdn.net/Thousa_Ho/article/details/72830054
• https://blog.csdn.net/wugemao/article/details/83826211