基本概念
布隆过滤器(Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的。它实际上是由一个很长的二进制向量(位向量)和一系列随机映射函数组成,布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率(假正例False positives,即Bloom Filter报告某一元素存在于某集合中,但是实际上该元素并不在集合中)和删除困难,但是没有识别错误的情形(即假反例False negatives,如果某个元素确实没有在该集合中,那么Bloom Filter 是不会报告该元素存在于集合中的,所以不会漏报)。因此,Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter通过极少的错误换取了存储空间的极大节省。
如果想判断一个元素是不是在一个集合里,一般想到的是将所有元素保存起来,然后通过比较确定。链表,树等等数据结构都是这种思路. 但是随着集合中元素的增加,我们需要的存储空间越来越大,检索速度也越来越慢。不过世界上还有一种叫作散列表(又叫哈希表,Hash table)的数据结构。它可以通过一个Hash函数将一个元素映射成一个位阵列(Bit Array)中的一个点。这样一来,我们只要看看这个点是不是 1 就知道可以集合中有没有它了。这就是布隆过滤器的基本思想。
Hash面临的问题就是冲突。假设 Hash 函数是随机的,如果我们的位阵列长度为 m 个点,那么如果我们想将冲突率降低到例如 1%, 这个散列表就只能容纳 m/100 个元素。显然这就不叫空间有效了(Space-efficient)。解决方法也简单,就是使用多个 Hash函数,如果它们有一个说元素不在集合中,那肯定就不在(必须对应位置上都是1)。如果它们都说在,有很小的可能性该元素不在。
BloomFilter的几个重要参数:
插入集合的元素个数n,BloomFilter位数组的长度m,hash函数个数k。
基本原理
布隆过滤器维护一个N位的位数组,其中N是位数组的大小。它还有另一个参数k,表示使用哈希函数的个数。这些哈希函数用来设置位数组的值。当往过滤器中插入元素x时,h1(x), h2(x), …, hk(x)所对应索引位置的值被置“1”,索引值由各个哈希函数计算得到。注意,如果我们增加哈希函数的数量,误报的概率会趋近于0.但是,插入和查找的时间开销更大,布隆过滤器的容量也会减小。
为了用布隆过滤器检验元素是否存在,我们需要校验是否所有的位置都被置“1”,与我们插入元素的过程非常相似。如果所有位置都被置“1”,那也就意味着该元素很有可能存在于布隆过滤器中。若有位置未被置“1”,那该元素一定不存在。
记录元素
下面我们看一下向Bloom Filter插入字符串的具体过,就是把这个字符串str经过K个不同的hash函数计算得到的结果h1、h2、、、hK。然后在BitArrray的第h1、h2、、、hK的位置上置1。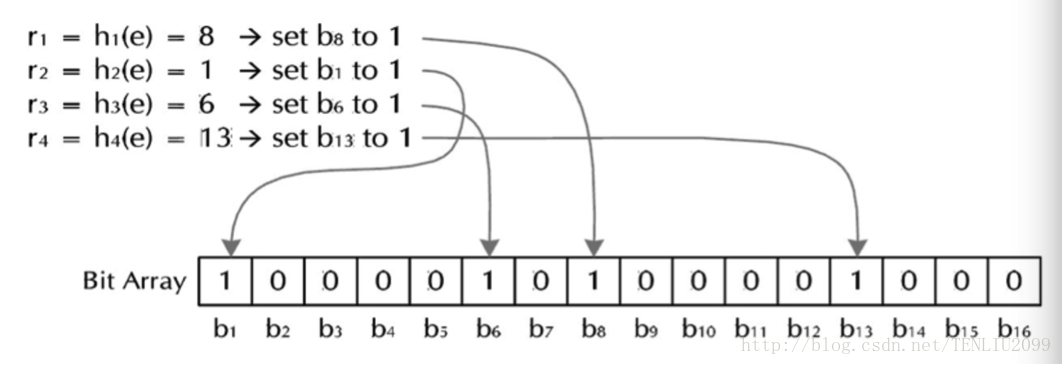
判断元素
那么如何判断一个字符串是否存在呢
把这个字符串经过K个hash函数计算得到h1、h2、、、hK,然后逐个判断BitArray的第h1、h2、、、hK个位置是否是1
影响误判率因素
只要降低Bloom Filter误判率,让它达到你可以接受的程度。BloomFilter当然就是你的利器了。影响它的因素有哪些呢?
- BitArray的位数M
- hash函数的数量K
- 每一个不同的hash函数的质量
优点:
1.全量存储但是不存储元素本身,在某些对保密要求非常严格的场合有优势
2.空间高效率
3.插入/查询时间都是常数O(k),远远超过一般的算法
缺点:
- 存在误算率(False Positive),随着存入的元素数量增加,误算率随之增加布隆过滤器能确保某个元素“肯定不存在”,但是对于一些元素的判断会是“可能存在”
- 一般情况下不能从布隆过滤器中删除元素
- 数组长度以及hash函数个数确定过程复杂
- 无法得到元素本身
- 布隆过滤器并不会保存插入元素的内容,只能检索某个元素是否存在
代码实现
1 | import BitVector as BitVector |
1 | from pybloom_live import ScalableBloomFilter,BloomFilter |