树的基本操作
1 | class TreeNode(object): |
二叉查找树(BST)
二叉查找树,Binary Search Tree,或者称为二叉搜索树。
性质:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 O(logn)
1 | class TreeNode(object): |
平衡二叉树(AVL):旋转耗时
在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
AVL树本质上还是一棵二叉搜索树,它的特点是:
- 本身首先是一棵二叉搜索树。
- 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
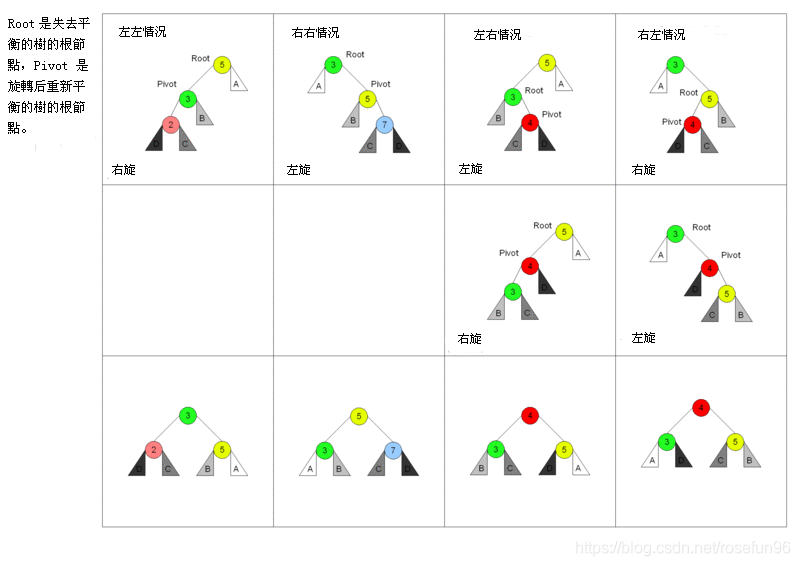
旋转
- 单向右旋平衡处理LL:由于在a的左子树根结点的左子树上插入结点,a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行一次右旋转操作;
- 单向左旋平衡处理RR:由于在a的右子树根结点的右子树上插入结点,a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行一次左旋转操作;
- 双向旋转(先左后右)平衡处理LR:由于在a的左子树根结点的右子树上插入结点,a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行两次旋转(先左旋后右旋)操作。
- 双向旋转(先右后左)平衡处理RL:由于在a的右子树根结点的左子树上插入结点,a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行两次旋转(先右旋后左旋)操作。
查找、插入和删除在平均和最坏情况下的时间复杂度都是O ( log n ) {\displaystyle O(\log {n})}O(logn).
由于旋转的耗时,AVL树在删除数据时效率很低;在删除操作较多时,维护平衡所需的代价可能高于其带来的好处,因此AVL实际使用并不广泛。
1 | class TreeNode(object): |
2-3-4树
2-3-4树是一种阶为4的B树。它是一种自平衡的数据结构,可以保证在O(lgn)的时间内完成查找、插入和删除操作。它主要满足以下性质:
(1)每个节点每个节点有1、2或3个key,分别称为2(孩子)节点,3(孩子)节点,4(孩子)节点。
(2)所有叶子节点到根节点的长度一致(也就是说叶子节点都在同一层)。
(3)每个节点的key从左到右保持了从小到大的顺序,两个key之间的子树中所有的
key一定大于它的父节点的左key,小于父节点的右key。
红黑树:树太高
2-3-4树和红黑树是完全等价的,由于绝大多数编程语言直接实现2-3-4树会非常繁琐,所以一般是通过实现红黑树来实现替代2-3-4树,而红黑树本也同样保证在O(lgn)的时间内完成查找、插入和删除操作。
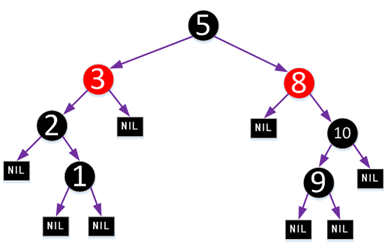
红黑树是每个节点都带有颜色属性的平衡二叉查找树 ,颜色为红色或黑色。除了二叉查找树一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是要么红色或要么是黑色。
- 根一定是黑色节点。
- 每个叶子结点都带有两个空的黑色结点(称之为NIL节点,它又被称为黑哨兵)。
- 每个红色节点的两个子节点都是黑色(或者说从每个叶子到根的所有路径上不能有两个连续的红色节点)。
- 从任一节点到它所能到达得叶子节点的所有简单路径都包含相同数目的黑色节点。
这些性质保证了根节点到任意叶子节点的路径长度,最多相差一半(因为路径上的黑色节点相等,差别只是不能相邻的红色节点个数),所以红黑树是一个基本平衡的二叉搜索树,它没有AVL树那么绝对平衡,但是同样的关键字组成的红黑树相比AVL旋转操作要少,而且删除操作也比AVL树效率更高,实际应用效果也比AVL树更出众。当然红黑树的具体实现也复杂的多。
B树
一个m阶的B树具有如下几个特征:B树中所有结点的孩子结点最大值称为B树的阶,通常用m表示。一个结点有k个孩子时,必有k-1个关键字才能将子树中所有关键字划分为k个子集。
- 根结点至少有两个子女。
- 每个中间节点都包含k-1个元素和k个孩子,其中 ceil(m/2) ≤ k ≤ m
- 每一个叶子节点都包含k-1个元素,其中 ceil(m/2) ≤ k ≤ m
- 所有的叶子结点都位于同一层。
- 每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分
- 每个结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)。其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。
Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。
n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。
查询
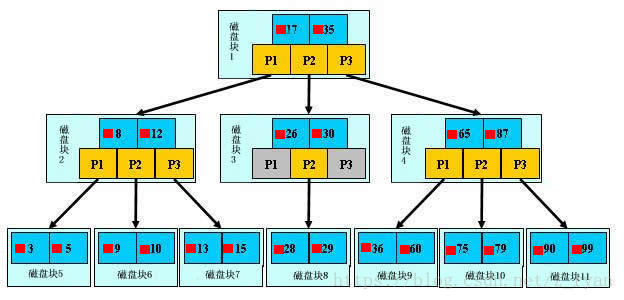
以上图为例:若查询的数值为5:
第一次磁盘IO:在内存中定位(与17、35比较),比17小,左子树;
第二次磁盘IO:在内存中定位(与8、12比较),比8小,左子树;
第三次磁盘IO:在内存中定位(与3、5比较),找到5,终止。
整个过程中,我们可以看出:比较的次数并不比二叉查找树少,尤其适当某一节点中的数据很多时,但是磁盘IO的次数却是大大减少。比较是在内存中进行的,相比于磁盘IO的速度,比较的耗时几乎可以忽略。所以当树的高度足够低的话,就可以极大的提高效率。相比之下,节点中的元素多点也没关系,仅仅是多了几次内存交互而已,只要不超过磁盘页的大小即可。
插入
对高度为k的m阶B树,新结点一般是插在叶子层。通过检索可以确定关键码应插入的结点位置。然后分两种情况讨论:
- 若该结点中关键码个数小于m-1,则直接插入即可。
- 若该结点中关键码个数等于m-1,则将引起结点的分裂。以中间关键码为界将结点一分为二,产生一个新结点,并把中间关键码插入到父结点(k-1层)中
重复上述工作,最坏情况一直分裂到根结点,建立一个新的根结点,整个B树增加一层。
B+树
B+树是对B树的一种变形,与B树的差异在于:
一个m阶的B+树具有如下几个特征:
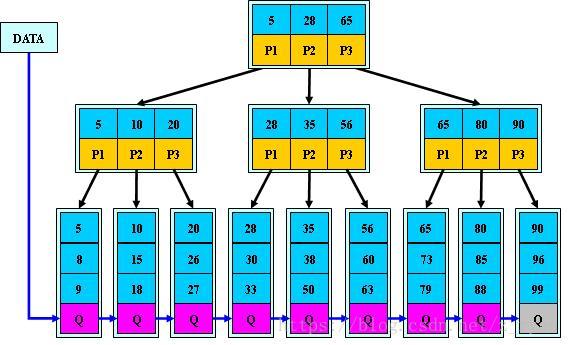
- 有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
- 所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
插入
B+树的插入与B树的插入过程类似。不同的是B+树在叶结点上进行,如果叶结点中的关键码个数超过m,就必须分裂成关键码数目大致相同的两个结点,并保证上层结点中有这两个结点的最大关键码。
删除
B+树中的关键码在叶结点层删除后,其在上层的复本可以保留,作为一个”分解关键码”存在,如果因为删除而造成结点中关键码数小于ceil(m/2),其处理过程与B-树的处理一样。在此,我就不多做介绍了。
B+树相比B树的优势:
- 单一节点存储更多的元素,使得查询的IO次数更少;
- 所有查询都要查找到叶子节点,查询性能稳定;
- 所有叶子节点形成有序链表,便于范围查询。
参考文章
- https://www.cnblogs.com/lliuye/p/9118591.html
- https://blog.csdn.net/qq_34364995/article/details/80787193
- https://www.jb51.net/article/166572.htm
- https://blog.csdn.net/rosefun96/article/details/108686365?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242
- https://blog.csdn.net/dongcai1905/article/details/101890478
- https://blog.csdn.net/u010853261/article/details/78217823
- https://blog.csdn.net/liangjiubujiu/article/details/84023736